kongruen dan kesebangunan

Kongruen adalah dua buah bangun datar yang memiliki panjang sisi, besar sudut, dan bentuk yang sama. Sedangkan, kesebangunan adalah dua buah bangun datar yang memiliki besar sudut dan bentuk yang sama tetapi, panjang sisi yang berbeda namun tetap dengan perbandingan yang senilai. Jadi, bangun yang sebangun belum tentu kongruen. tetapi, bangun yang kongruen pasti sebangun.

Ada 4 cara untuk mengetahui bahwa segitiga tersebut kongruen:

1. SSS- Side Side Side (sisi sisi sisi) = artinya segitiga yang memiliki 3 sisi yang sama panjang

AB=EF (S)

AC=EG (S)
BC=FG (S)

   
 
     2. SAS- Side Angle Side (sisi sudut sisi)= artinya segitiga yang memiliki 2 sisi yang sama panjang dan diantaranya ada sudut yang sama besar

AB=EF (S)

LBAC=LFEG (A)

AC=EG (S)

       3. AAS- Angle Angle Side (sudut sudut sisi)= artinya segitiga yang memiliki 2 sudut yang sama besar dan 1 sisi yang sama panjang dan bersesuaian

LEDF=LKJL (A)

LDEF=LJKL (A)

DE=JK (S)

        4. RHS- Right Angle Hypotenuse Side (sudut sisi sisi)= artinya memiliki sudut siku-siku dan 2 sisi yang sama panjang

LABC=LMNO

AC=MO

BC=NO

Ada 3 cara untuk mengetahui bahwa segitiga tersebut sebangun:

1. AA- Angle Angle (sudut sudut)= artinya memiliki 2 sudut yang sama besar

LBAC=LKPL (A)

LABC=LPKL (A)

         2. SSS- Side Side Side (sisi sisi sisi)= artinya memiliki 3 sisi yang mepunyai perbandingan yang bersesuaian/sama

DB:MK = 8 CM : 4 CM= 2 (S)

BC:KL = 6 CM : 3 CM= 2 (S)

DC:ML = 8 CM : 4 CM= 2 (S)

              3. SAS- Side Angle Side ( sisi sudut sisi)= artinya memiliki 2 sisi yang mempunyai perbandingan yang bersesuaian/sama dan memiliki 1 sudut yang sama besar

DK:MG= 12 CM: 4 CM= 3 (S)

LKDH=LGMJ (A)

KH;GJ= 9 CM : 3 CM= 3 (S)

CONTOH SOAL

1.  Buktikanlah bahwa segitiga di bawah ini kongruen!

Pembahasan:  BL= KJ (S)

                       BK= LJ (S)

                       KL1= KL2 (S)

       Jadi, segitiga BKL (segitiga 1) kongruen dengan segitiga LKJ (segitiga 2)

2. Buktikanlah bahwa segitiga di bawah ini kongruen!

Pembahasan: DL=LG (S)

                      LDLO=LHLG (A)* Sudut yang berhadapan mempunyai besar sudut yang sama

                      HL=LO (S)

      

     Jadi, segitiga DLG kongruen dengan segitiga HLG

Kesebangunan di segitiga siku-siku

1. luas segitiga 

    1/2 . PD . PR = 1/2 . PS. SR  

              PD.PR = PS.SR

2. DP ² = DS . DR

3. PR ² = SR . DR

4. PS ² = SR . DS

           DP:DS = DR: DP                          PR:SR = RD:PR                SP:SR = DS:PS                  

                DP2 = DS.DR                             PR2 = SR.DR                   PS2 = SR.DS

                 

Contoh Soal 

1.  X = ......

          PEMBAHASAN

                      5:9 = 7.4 : 7.4 + X

              37 + 5X = 66.6

                       5X= 29.6

                            X = 5.92 CM

2. 

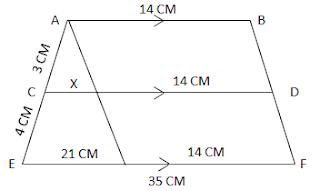
CD = .....

PEMBAHASAN

JADI, BUATLAH GARIS BANTU DI DALAM TRAPESIUM INI YANG MEMBENTUK SEBUAH SEGITIGA UNTUK DAPAT MEMBANDINGKAN SEGITIGA KECIL TERSEBUT DENGAN SEGITIGA YANG BESAR

CD = X + 14

3:7 = X : 21

 7X = 63

   X = 9 CM

CD = 9 + 14

      = 23 CM